Picking up threads from previous posts on solving Semantle word puzzles with machine learning, we’re ready to explore how different solvers might play along with people while playing the game online. Maybe you’d like to play speed Semantle against an artificially intelligent opponent, maybe you’d like a left-of-field hint on a tricky puzzle, or maybe it’s just fun to spectate at a cerebral robot battle.
Substitute semantics
The solvers have a view of how words relate due to a similarity model that is encapsulated for ease of change. To date, we’ve used the same model as live Semantle, which is word2vec. But as this might be considered cheating, we can now also use a model based on the Universal Sentence Encoder (USE), to explore how the solvers perform with separated semantics.
Solver spec
To recap, the key elements of the solver ecosystem are now:
- SimilarityModel – choice of word2vec or USE as above,
- Solver methods (common to both gradient and cohort variants):
- make_guess() – return a guess that is based on the solver’s current state, but don’t change the solver’s state,
- merge_guess(guess, score) – update the solver’s state with information about a guess and a score,
- Scoring of guesses by either the simulator or a Semantle game, where a game could also include guesses from other players.
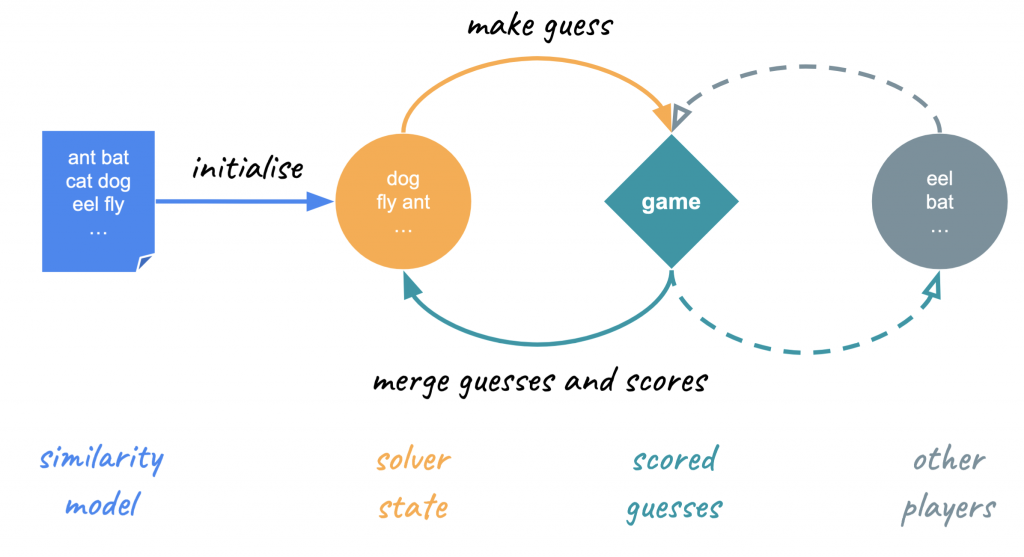
It’s a simplified reinforcement learning setup. Different combinations of these elements allow us to explore different scenarios.
Solver suggestions
Let’s look at how solvers might play with people. The base scenario friends is the actual history of a game played with people, completed in 109 guesses.
Word2Vec similarity
Solvers could complete a puzzle from an initial sequence of guesses from friends. Both solvers in this particular configuration generally easily better the friends result when primed with the first 10 friend guesses.
Solvers could instead make the next guess only, but based on the game history up to that point. Both solvers may permit a finish in slightly fewer guesses. The conclusion is that these solvers are good for hints, especially if they are followed!
Maybe these solvers using word2vec similarity do have an unfair advantage though – how do they perform with a different similarity model? Using USE instead, I expected the cohort solver to be more robust than the gradient solver…
USE similarity
… but it seems that the gradient descent solver is more robust to a disparate similarity model, as one example of the completion scenario shows.
The gradient solver also generally offers some benefit making a suggestion for just the next guess, but the cohort solver’s contribution is marginal at best.
These are of course only single instances of each scenario, and there is significant variation between runs. It’s been interesting to see this play out interactively, but a more comprehensive performance characterisation – with plenty of scope for understanding the influence of hyperparameters – may be in order.
Solver solo
The solvers can also play part or whole games solo (or with other players) in a live environment, using Selenium WebDriver to submit guesses and collect scores. The leading animation above is gradient-USE and a below is a faster game using cohort-word2vec.
So long
And that’s it for now! We have multiple solver configurations that can play online by themselves or with other people. They demonstrate how people and machines can collaborate to each bring their own strengths to solving problems; people with creative strategies and machines with a relentless ability to crunch through possibilities. They don’t spoil the fun of solving Semantle yourself or with friends, but they do provide new ways to play and to gain insight into how to improve your own game.
Postscript: seeing in space
Through all this I’ve considered various 3D visualisations of search through a semantic space with hundreds of dimensions. I’ve settled on the version below, illustrating a search for target “habitat” from first guess “megawatt”.
This visualisation format uses cylindrical coordinates, broken out in the figure below. The cylinder (x) axis is the projection of each guess to the line that connects the first guess to the target word. The cylindrical radius is the distance of each guess in embedding space from its projection on this line (cosine similarity seemed smoother than Euclidian distance here). The angle of rotation in cylindrical coordinates (theta) is the cumulative angle between the directions connecting guess n-1 to n and n to n+1. The result is an irregular helix expanding then contracting, all while twisting around the axis from first to lass guess.








